Oh wow, A3 is one tough assignment! Since number one is just pigeonhole principle; question two is just some algebra and nothing else special; question three is something from the textbook (204) -- this makes question 4 ridiculously hard and long.
Here are some thoughts for question 4 which I was thinking about:
CSC236's Blog
Sunday, December 2, 2012
Saturday, November 24, 2012
A good reading from WikiBooks
Artical from: http://en.wikibooks.org/wiki/Logic_for_Computer_Scientists/Introduction
Please try not to repost this article somewhere else! thanks --gcseed
In order to define datatypes and to derive efficient implementations for it, the concept of abstract datatype definitions is central. The idea is to define the abstract properties of a datatype, instead of giving special realisations. A very trivial example is the definition of a stack: Let 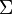 be an alphabet. In order to define a stack
be an alphabet. In order to define a stack  over
over 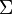 we assume
we assume 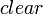 to be a nullary function and we define the following properties of stacks:
to be a nullary function and we define the following properties of stacks:
 be an alphabet. In order to define a stack
be an alphabet. In order to define a stack  over
over 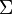 we assume
we assume 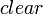 to be a nullary function and we define the following properties of stacks:
to be a nullary function and we define the following properties of stacks: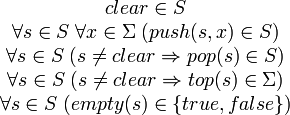
Hence, we have the functions  and
and 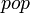 , which yield stacks and the predicate
, which yield stacks and the predicate 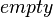 , furthermore we need the following properties with respect to the
, furthermore we need the following properties with respect to the 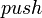 -operation.
-operation.
 and
and 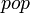 , which yield stacks and the predicate
, which yield stacks and the predicate 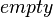 , furthermore we need the following properties with respect to the
, furthermore we need the following properties with respect to the 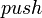 -operation.
-operation.
And we have to give properties with respect of the combinations of functions:
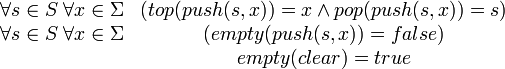
The above formulae state what properties we expect stacks to have. Obviously it contains no hints how to implement such a data type. And indeed this specification is aiming to solve other problems, e.g.
- Is the specification correct? I.e. is there a set
 together with the given operations, such that the axioms above hold?
together with the given operations, such that the axioms above hold? - Is the specification complete. I.e. do the axioms imply all the properties we intuitively assume a stack to have? Are there sets
 which do not meet our expectations?
which do not meet our expectations?
The reader may have already noticed, that the axioms are nothing else than formulas in predicate logic, i.e. all logic where variables like  or
or  together with so called quantifiers
together with so called quantifiers 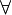 and
and 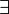 are used. The above two questions, namely correctness and completeness, are very central topics for the design of formal systems in logic. The proof of these properties often is difficult and costly, but on the other hand it is one of the clear advantages of logical systems, that these properties can be proved formally. In the main part of this course we will deal with these questions explicitly.
are used. The above two questions, namely correctness and completeness, are very central topics for the design of formal systems in logic. The proof of these properties often is difficult and costly, but on the other hand it is one of the clear advantages of logical systems, that these properties can be proved formally. In the main part of this course we will deal with these questions explicitly.
 or
or  together with so called quantifiers
together with so called quantifiers 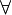 and
and 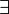 are used. The above two questions, namely correctness and completeness, are very central topics for the design of formal systems in logic. The proof of these properties often is difficult and costly, but on the other hand it is one of the clear advantages of logical systems, that these properties can be proved formally. In the main part of this course we will deal with these questions explicitly.
are used. The above two questions, namely correctness and completeness, are very central topics for the design of formal systems in logic. The proof of these properties often is difficult and costly, but on the other hand it is one of the clear advantages of logical systems, that these properties can be proved formally. In the main part of this course we will deal with these questions explicitly.Friday, November 23, 2012
Missed A2
Since I have missed my 2nd assignment of the course, I will do Q2 here instead
P(n): for every positive integer m, if m < n then T(m) ≤ T(n)
Using complete induction prove that P(n) holds for all integers n ≥ 1
Let k be an arbitrary integer such that k ≥ 1. Now suppose that P(β) holds for all integers β such that 1 ≤ β < k.
Then prove that P(k) holds as well.
By cases:
Case 1. k = 1. P(1) holds trivially since there is no positive integer m < 1.
Case 2. k = 2. T(1) and T(2)
T(1) = 1
T(2) = 1 + max{T(1), T(1)} = 1 + T(1) = 2
Since T(1) < T(2) then P(2) holds!
Case 3. k > 2.
In this case, 1 ≤ (k – 1) < k and, by Lemma 3.3 (in the course notes), 1 ≤ ⌊k/2⌋ ≤ ⌈k/2⌉ < k.
Therefore, by induction hypothesis, P(k − 1), P(⌊k/2⌋) and P(⌈k/2⌉) all hold. Since P(k − 1) holds, to prove that P(k) holds as well, it suffices to prove that T(k − 1) ≤ T(k).
So,
T(k – 1) = 1 + max{ T(⌈(k-1)/2⌉),
T(⌊(k-1)/2⌋) }
≤ 1 + max{ T(⌈k/2⌉), T(⌊k/2⌋) }
= T(k)
T(k – 1) ≤ T(k)
Friday, November 16, 2012
An easy question from the past assignment, and some others
1. P(n): n3
+ n < 3n. I will prove that P(n)
is true for every natural number. (IH)
#
I observe that from P(4) and beyond,
it is always true.
Proof
(by Mathematical Induction)
Base Case: n
< 4: P(n) for n
{0,1,2,3}. From the
chart above, it is easy to tell that P(n)
is false for n
{2,3}, so none of these two values can
be reached using the logic of the induction step.
Induction Step: Assume
n
ℕ
- {0,1,2,3}
and that P(n) is true.
Then
3
· P(n) = 3 · (n3 + n) <
3 · 3n # times 3 on both
sides
n3 + n3 + n3 + 3n < 3n+1
And
from IH, P(n+1) = (n+1)3 +
(n + 1) < 3n+1
= n3 + 3 · n2
+ 4n +2 < 3n+1
Since:
n3 = n3
n3
> 3 · n2
# n is natural number – {0,1,2,3}, which means n > 3
n3 >
4n # n is natural number – {0,1,2,3}, which means n > 3
3n > 2 # n is natural number – {0,1,2,3}, which means n > 3
Then n3 + n3 + n3 +
3n > n3 + 3 · n2 + 4n +2 ⇒ 3 · P(n) > P(n+1)
So that we can conclude: 3
· 3n > 3 · P(n) > P(n+1) ⇒
3n+1 > P(n+1)
So
P(n+1) follows
Since I assumed n is a generic natural number greater
than 3, ∀n
ℕ
- {0,1,2,3}, P(n) ⇒ P(n+1).
I conclude ∀n
ℕ
- {0,1,2,3}, P(n), by Mathematical Induction.
Saturday, November 3, 2012
I am back in Toronto!
I applied the Master theorem to a recurrence for a running time I encountered
However, this hides a constant dependent on r in the big-oh notation: our recurrence has depth O(log2n) so at the final level we have O(4log2n)=O(n2) subproblems, each of which takes O(r) time to be handled. This means the actual running time is O(n2r) (or worse: this analysis only talks about the lowest level).
This is my actual recursion:
Sunday, October 21, 2012
Leaving Toronto for awhile!
Since there's some personal issues, I will be leaving Toronto for about 10 days. That since Blogger does not work in China (blocked like facebook and youtube), which means I will not be update my SLOG for about 13 days. See you all when I am back!
Saturday, October 20, 2012
Some thoughts after the midterm
First of all, I have to say reading the questions carefully is more important than understanding the question. e.g. Q2 on the midterm, the question was asking number of leaves instead of number of total nodes in the tree, which makes the question lot easier by only asking the lowest level of the tree. From the observation, the worst-case is when we have a full binary tree, where it's lowest level always has 2^(n-1) leaves.
Second, any non-full binary trees will be smaller than full binary trees, therefore we can prove in both cases, P(n) is true!
Subscribe to:
Posts (Atom)






